曲线点阵

利用一元N次曲线方程求解得到曲线方程，如何让物体按照曲线的运行。有两种方式

• 实时计算点的下一个坐标，返回给运动单元。此方式简单的计算并不会影响性能，但难以控制运行速度，因为曲线的斜率是变化的。详看下面题外篇。

• 初始化时将所有点采集到集合，通过移动下标的方式返回坐标给运动单元。

采点间隔

已知起始点、目标点、以及两点之间的曲线方程，采点间隔按需要可分为两种：固定插入点数量、保持一定间距插入任意点数量。

以固定点数插入点阵，（帧率固定）。其中sa为一元N次方程系数，插入针数ideaFrame=50。

for (int j = 0; j < ideaFrame; j++) {
	double xx = oriPoints[i].x + (randx - oriPoints[i].x) / ideaFrame * (j + 1);
	double yy = 0;
	for (int m = 0; m < sa.size(); m++) {
		yy += sa[m] * pow(xx, m);
	}
	this->dance_frame[j].push_back(Node(xx, yy));
}

以固定横坐标间距插入点阵跟上面类似。

椭圆方程如何处理

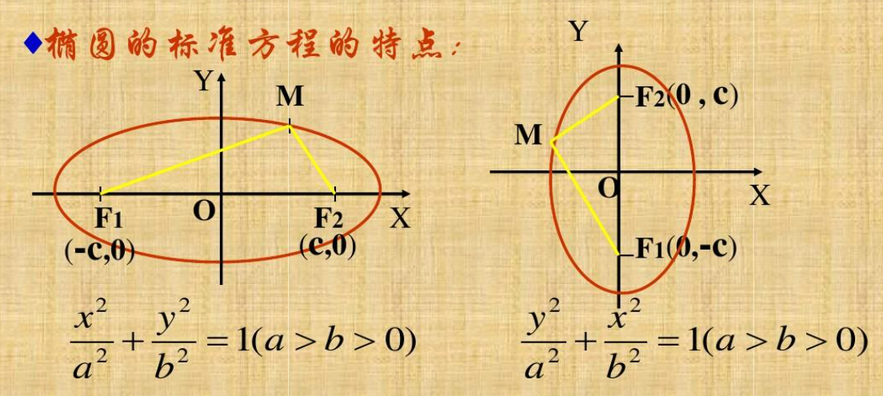
椭圆按横坐标或者纵坐标采点需要区分上下，根据圆心点坐标计算采点的坐标正负。通过两次for循环从左往右然后从右往左直到回到原点附近。

题外篇

二维坐标系下的旋转公式

让椭圆旋转起来

Node MyRotate(Node nodeX, Node node2, double rorate) {
	return Node((node2.x - nodeX.x)*(cos(rorate*3.14159 / 180)) - (node2.y - nodeX.y)*(sin(rorate*3.14159 / 180)) + nodeX.x, (node2.y - nodeX.y)*(cos(rorate*3.14159 / 180)) + (node2.x - nodeX.x)*(sin(rorate*3.14159 / 180)) + nodeX.y);
}

变化的斜率导致运动速度不一致问题如何解决

如图，在椭圆左右两边移动速度过快

这种情况下，如果已知曲线的特性，可以根据象限来判断采样以横坐标采样还是以纵坐标采样。根据象限采样优化后的效果如下。

如果曲线是随机生成的，那么可以根据斜率决定采样横纵坐标以及采样距离，这样的过程就比较复杂。